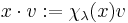Harish-Chandra isomorphism

Not to be confused with Harish-Chandra homomorphism.

In mathematics, the Harish-Chandra isomorphism, introduced by Harish-Chandra (1951), is an isomorphism of commutative rings constructed in the theory of Lie algebras. The isomorphism maps the center Z(U(g)) of the universal enveloping algebra U(g) of a reductive Lie algebra g to the elements S(h)^W of the symmetric algebra S(h) of a Cartan subalgebra h that are invariant under the Weyl group W.

1 Fundamental invariants
2 Examples
3 Introduction and setting
- 3.1 Central characters
4 Statement of Harish-Chandra theorem
5 Applications
6 See also
7 References

Fundamental invariants

Let n be the rank of g, which is the dimension of the Cartan subalgebra h. H. S. M. Coxeter observed that S(h)^W is a polynomial algebra in n variables (see Chevalley–Shephard–Todd theorem for a more general statement). Therefore, the center of the universal enveloping algebra of a reductive Lie algebra is a polynomial algebra. The degrees of the generators are the degrees of the fundamental invariants given in the following table.

Lie algebra	Coxeter number h	Dual Coxeter number	Degrees of fundamental invariants
R	0	0	1
A_n	n + 1	n + 1	2, 3, 4, ..., n + 1
B_n	2n	2n − 1	2, 4, 6, ..., 2n
C_n	2n	n + 1	2, 4, 6, ..., 2n
D_n	2n − 2	2n − 2	n; 2, 4, 6, ..., 2n − 2
E₆	12	12	2, 5, 6, 8, 9, 12
E₇	18	18	2, 6, 8, 10, 12, 14, 18
E₈	30	30	2, 8, 12, 14, 18, 20, 24, 30
F₄	12	9	2, 6, 8, 12
G₂	6	4	2, 6

For example, the center of the universal enveloping algebra of G₂ is a polynomial algebra on generators of degrees 2 and 6.

Examples

If g is the Lie algebra sl₂(R), then the center of the universal enveloping algebra is generated by the Casimir invariant of degree 2, and the ring of invariants of the Weyl group is also generated by an element of degree 2.

Introduction and setting

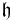Let $\mathfrak{g}$ be a semisimple Lie algebra, $\mathfrak{h}$ its Cartan subalgebra and 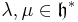$\lambda, \mu\in\mathfrak{h}^*$ be two elements of the weight space and assume that a set of positive roots 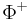$\Phi^%2B$ have been fixed. Let 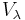$V_\lambda$ , resp. 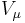$V_\mu$ be highest weight modules with highest weight $\lambda$ , resp. $\mu$ .

Central characters

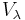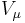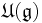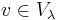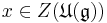The $\mathfrak{g}$ -modules $V_\lambda$ and $V_\mu$ are representations of the universal enveloping algebra $\mathfrak{U}(\mathfrak{g})$ and its center acts on the modules by scalar multiplication (this follows from the fact that the modules are generated by a highest weight vector). So, for $v\in V_\lambda$ and $x\in Z(\mathfrak{U}(\mathfrak{g}))$ ,

$x\cdot v:=\chi_\lambda(x)v$

and similarly for 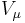$V_\mu$ .

The functions 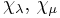$\chi_\lambda, \,\chi_\mu$ are homomorphims to scalars called central characters.

Statement of Harish-Chandra theorem

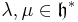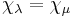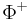For any $\lambda,\mu\in\mathfrak{h}^*$ , the characters $\chi_\lambda=\chi_\mu$ if and only if $\lambda$ and $\mu$ are on the same orbit of the Weyl group of $\mathfrak{g}$ under the affine action (corresponding to the choice of the positive roots $\Phi^%2B$ ).

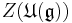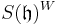Another closely related formulation is that the Harish-Chandra homomorphism from the centrum of the universal enveloping algebra $Z(\mathfrak{U}(\mathfrak{g}))$ to $S(\mathfrak{h})^W$ (invariant polynomials over the Cartan subalgebra fixed by the affine action of the Weyl group) is an isomorphism.

Applications

The theorem may be used to obtain a simple algebraic proof of Weyl's character formula for finite dimensional representations.

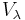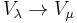Further, it is a necessary condition for the existence of a nonzero homomorphism of some highest weight moules (a homomorphism of such modules preserves central character). A simple consequence is that for Verma modules or generalized Verma modules $V_\lambda$ with highest weight $\lambda$ , there exist only finitely many weights $\mu$ such that a nonzero homomorphism $V_\lambda\to V_\mu$ exists.

References

Harish-Chandra (1951), "On some applications of the universal enveloping algebra of a semisimple Lie algebra", Transactions of the American Mathematical Society 70: 28–96, ISSN 0002-9947, JSTOR 1990524, MR 0044515
Humphreys, James E. (2000), Introduction to Lie algebras and representation theory, Birkhäuser, p. 126, ISBN 978-0387900537
Humphreys, James E. (2008), Representations of semisimple Lie algebras in the BGG category O, AMS, p. 26, ISBN 978-0821846780

Knapp, Anthony W.; Vogan, David A. (1995), Cohomological induction and unitary representations, Princeton Mathematical Series, 45, Princeton University Press, ISBN 978-0-691-03756-1, MR 1330919
Knapp, Anthony, Lie groups beyond an introduction, Second edition, pages 300–303.